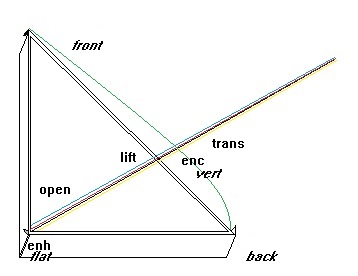
painting in layers according to a predefined and rigorous
model
Instead of painting from life and observation it is possible to construct a painting according to a strategy only, working from the inside out.
A strategy is more than a set of techniques, it presents a take on things, a model, where certain aspects are ignored and others emphasised.
As animals differ from plants by the fact that they can move around in space, so do humans differ from animals by the fact that they can formulate intent and plan ahead.
Painting lends itself perfectly to this end: to formulate and realize a precise intent. When the model here proposed is applied with grace, it can present the subject as if the light radiates from within rather than light being cast upon it.
The subject becomes 'de igne' -made of fire.
It resides in an afterlife of some sort,
where the natural laws are reversed or non-existent. This happens to be one of the main ideas behind traditional icon painting, from which western art has borrowed so much: to throw a window onto a netherworld, a world of worship reachable only through transcendence. Similar to an icon, the work is to suggest grace, refinement, sanctity, humility, simplicity and calm. This both by the selected subject matter as by the way in which it is made: through a precisely defined process requiring devotion and measurement...
the rule of three
Paint is a mixture that is made up of three types of ingredients: pigments that give the paint its color, binders that keep the pigments in place after drying
and solvents that thin the paint, lower its strength and make it flow. Other types of ingredients may exist, such as siccatives or retardants but they are not relevant to the concepts explained here.
Working by example, the first thing we will do is measure these three types of ingredients on a weighing scale before we mix them to make a paint. Say we put 4 mg of mars black, 30 mg of egg tempera and 480 mg of water together, it gives us 514 mg of paint in total.
|
Feo
Mars noir
|
Egy
Egg yolk
|
H2O
Distilled water
|
|---|---|---|
| 4 mg | 30 mg | 480 mg |
In order to find the percentile quantities of this mixture we must do no more than apply the rule of three to each ingredient, where B is the ingredient quantity, A is the total quantity 514 and C is 100. x = (B/A)*C.
This will give us approximately:
- mars black: (4/514)*100 ≈ 0.77%
- tempera: (30/514)*100 ≈ 13.33%
- water: (480/514)*100 ≈ 85,9%
|
Feo
Mars noir
|
Egy
Egg yolk
|
H2O
Distilled water
|
|---|---|---|
| 0.77% | 13.33% | 85.9% |
The rule of three extracts a ratio of B to A, and applies this ratio to a pair of which only one variable is known, C, in order to get x.
properties of interest
So far, this gives us some properties of the paint that we can already work with. We can store the recipe in percentile form and use the rule of three to recreate this exact recipe at a later time in any quantity.
In order to make 650 mg of our recipe, we mix approximately:
- mars black: (0.77/100)*650 ≈ 5 mg
- tempera: (13.33/100)*650 ≈ 87 mg
- water: (85.9/100)*650 ≈ 557 mg
A similar method is applied in the kitchen when making pancakes for 10 people from a base recipe for 5. However, percentile quantities do not tell us all we want to know about a certain mixture when this mixture is to be used underneath or on top of other paint layers. We will now proceed to define a set of properties that tell us all we want to know about a mixture when it is used as an element in an overall model.
power and temper
The most important properties of paint are power and temper. With only these two we would already be able to say a great deal about any mixture we choose to make:- Power (pow) is the sum of all pigment percentiles
- Temper (tem) is the ratio of the amount of binder to the the sum of all pigments
The notation we will use for this is pow|tem.
To calculate the power property of our previous example, we can simply take the percentile amount of mars black because it's the only pigment in the mixture, so pow = 0.77. To calculate the temper property we must divide the percentile amount of binder by the percentile amount of pigment,so 13.33/0.77 ≈ 17.31.
In the notation we will quote the pigment code before the numbers, so the final notation for our previous example will be Feo: .77|17. With this notation we lose some accuracy, but it will still be accurate enough. We will calculate quantities starting from the values of the properties, and not the other way around as we have done above.
In order to make 650 mg of our so called Feo: .77|17, we mix approximately:
- mars black: (0.77/100)*650 ≈ 5 mg
- tempera: ((0.77*17)/100)*650 ≈ 85 mg
- water: 650-5-85 = 560 mg
When multiple pigments and binders are used in a mixture, we will have to extend on the notation and the calculations quite a bit, but before we get more geeky about paint let's explore some basic concepts we wish to monitor when making all these calculations. Hopefully it will make more sense as to why anyone would even want to go through this trouble in the first place.
rock paper scissors
After defining power and temper I might as well introduce a third property called flow:
- Flow (flow) is the solvent percentile
- When pow increases, tem goes down
- When tem increases, flow goes down
- When flow increases, pow goes down
fat over lean
Most artists will at some point in their education have heard of the 'fat over lean' rule. But there is often some confusion about what it implies exactly.For a long time I thought I was painting fat over lean when I would dilute the first layers with a solvent and then use more and more paint directly from the tube as I painted on. This is off course not the case, because the fatness or amount of binder in this process remains proportionally the same. Solvents evaporate so to use more or less of them does not influence the composition of what is left behind.
Fat over lean means that the proportion of binder to pigment goes up as you go up the layers. Cracks in a surface will appear when a more brittle layer is placed on top of a more flexible layer. So to state the fat over lean rule in the reverse way: in order to create stable layers the brittleness of the mixtures must keep on decreasing as you add new layers. How would one define brittleness? Imagine a block of concrete as a mixture of cement and pebbles. If it would have too many pebbles, it would be easier to chip off a piece with a hammer. So the proportion of cement to pebbles would define the brittleness. In our case, the ratio of binder to pigment would define the brittleness. So to conclude, the "tem" property as defined above is not so much a matter of taste as it is a technical restriction, it must have a certain value in order to guarantee stability.
scalability
A system can be considered scalable when there is no need to change the way it is set up when certain key parameters are tweaked. In our case, scalability refers to the "slicing" of the layers in the model. Let us work from another example using vermillion imitation(Ver).To make 800 mg of Ver: 2.0|8.0, we will mix approximately:
- vermillion: (2.0/100)*800 = 16 mg
- tempera: ((2.0*8.0)/100)*800 = 128 mg
- water: 800-16-128 = 656 mg
|
Egy
Egg yolk
|
H2O
Distilled water
|
|
|---|---|---|
| 2% | 16% | 82% |
The amount of color left behind by this process might be expressed by multiplying power by the number of layers 2*3 = 6. Which brings us right away to the definition of another property: result.
- Result (res) is power multiplied by the number of layers
In order to scale this process up, we will choose to apply the color in more consecutive layers while keeping the original result value of 6. This will yield, at least in theory, a more refined look without changing how much paint is deposited. So to upscale our process to six layers we will choose a power of 1, while keeping a result of 6, res/n = pow, 6/6 = 1.
To make 800 mg of Ver: 1.0|8.0, we will mix approximately:
- vermillion: (1.0/100)*800 = 8 mg
- tempera: ((1.0*8.0)/100)*800 = 64 mg
- water: 800-8-64 = 728 mg
|
Egy
Egg yolk
|
H2O
Distilled water
|
|
|---|---|---|
| 1% | 8% | 91% |
Notice that the tem property remains the same, because it is a ratio, only power needs to be recalculated when re-scaling. Similarly, we can choose to downscale the process, yielding a more brutal and direct look. If we choose to apply the result in two layers, the power of our recipe will be 6/2 = 3.
To make 800 mg of Ver: 3.0|8.0, we will mix approximately:
- vermillion: (3.0/100)*800 = 24 mg
- tempera: ((3.0*8.0)/100)*800 = 192 mg
- water: 800-24-192 = 584 mg
|
Egy
Egg yolk
|
H2O
Distilled water
|
|
|---|---|---|
| 3% | 24% | 73% |
Each of these three processes will in the end have deposited the same amount of colour and binder. The concept of scalability is especially important in projects that take a long time to complete. Often when making a drawing, after only a few hours you will notice that there is nothing more you can add to make it better, only worse. The point of saturation is reached quite quickly, no amount of labour on your part can then add more value. I would call this the Francis-point after my fantastic drawing teacher Filip Francis who stated "When is a drawing finished? Just before you finished it, it was finished -but you didn't see it!".
Painting is extremely well suited to push the Francis-point back endlessly, for months and even years, if only the quantities are carefully monitored throughout. In theory it would be possible to work on a painting for hundreds of years passing it on for generations like a bonsai tree or a dog breed. Scaling-up therefore is a tactic that allows labour to keep being converted into value. That being said, there are restrictions as to how much you can actually dilute a paint before the absolute amount of binder in the mixture becomes too low to perform its job.
b:a and c:a
Now that we have explored some basic concepts we can start working with multiple pigments in a mixture. Apart from whites, we will never mix more than 3 pigments into a recipe. This keeps the colors clear and crisp. We will call these three pigments a, b and c where a is the main pigment to which the others will be defined relatively. To give the three non-white pigments a place in the system, we will introduce 2 more properties.
- b ratio (b:a) is the ratio of the amount of b pigment to the amount of a pigment
- c ratio (c:a) is the ratio of the amount of c pigment to the amount of a pigment
Let us start then by putting lion green, sienna natural and burnt umber together:
- 15 mg of lion green: (15/1000)*100 = 1.5%
- 5 mg of sienna natural: (5/1000)*100 = 0.5%
- 20 mg of burnt umber: (20/1000)*100 = 2%
- 200 mg of tempera: (200)/1000)*100 = 20%
- 760 mg of water: (760)/1000)*100 = 76%
|
Grl
Vert lion
|
Sina
Sienna nat
|
Egy
Egg yolk
|
H2O
Distilled water
|
|
|---|---|---|---|---|
| 1.5% | 0.5% | 2% | 20% | 76% |
The power of this mixture is the sum of all pigment percentiles 1.5+0.5+2 = 4, the temper is 20/4 = 5. To capture the relative distribution of pigments within that 4% we must calculate b:a which is 0.5/1.5 ≈ 0.33 and c:a which is 2/1.5 ≈ 1.33. Before we reverse engineer this recipe starting from the properties, let's look at the notation, which should speak for itself Grl-Sina-Bu: 4.0|5.0 b.33 c1.3.
Now let us go ahead and make 2000 mg of Grl-Sina-Bu: 4.0|5.0 b.33 c1.3:
- lion green: ((1/(1+0.33+1.3)*4.0)/100)*2000 ≈ 30 mg
- sienna natural: ((0.33/(1+0.33+1.3)*4.0)/100)*2000 ≈ 10 mg
- burnt umber: ((1.3/(1+0.33+1.3)*4.0)/100)*2000 ≈ 40 mg
- tempera: ((4.0*5.0)/100)*2000 ≈ 400 mg
- water: 2000-30-10-40-400 ≈ 1520 mg
luminosity
Luminosity is the final property we need to define in order to have the full notation and calculation. We will first proceed to demonstrate this property with a single base pigment before we introduce b:a and c:a. As we mentioned before, we will never mix more than 3 pigments into a recipe, -apart from whites. White pigments such as titanium white, zinc white or lead white are a class apart because they bring special qualities to the paint. That is why they have their own property which is a ratio that sits on top of a,b and c pigments instead of alongside them. So let's define this property exactly:
- Luminosity (lum) is the ratio of all white pigments to all other pigments
Again as in our previous examples we will first make a mixture to see what the value of the property would be and later work backwards, starting from the properties and then mix by a formula.
Let's get on and mix some paint containing permanent blue dark and titanium white.
- 40 mg of permanent blue dark: (40/2000)*100 = 2%
- 30 mg of titanium white: (30/2000)*100 = 1.5%
- 560 mg of tempera: (560)/2000)*100 = 28%
- 1370 mg of water: (1370)/2000)*100 = 68.5%
The power is 2+1.5 = 3.5, the temper is 20/2.5 = 8. The luminosity then would be 1.5/2 = 0.75. The notation is Bpf: 3.5|8.0 ∝.75.
Let us go ahead and make 3000 mg of Bpf: 3.5|8.0 ∝.75:
- permanent blue dark: ((1/(1+0.75)*3.5)/100)*3000 = 60 mg
- titanium white: ((0.75/(1+0.75)*3.5)/100)*3000 = 45 mg
- tempera: ((3.5*8.0)/100)*3000 = 840 mg
- water: 3000-60-45-840 = 2055 mg
|
Bpf
Bleu perm fonce
|
Tit
Titanium white
|
Egy
Egg yolk
|
H2O
Distilled water
|
|---|---|---|---|
| 2% | 1.5% | 28% | 68.5% |
Now let's reintroduce b:a and c:a to see the full calculation of all properties in one example.
Let's make 5000 mg Grl-Sina-Lem: 4.0|8.0 ∝.75 b0.5 c1.5:
- lion green: ((1/(1+0.75)*(1/(1+0.5+1.5))*4.0)/100)*5000 ≈ 38 mg
- sienna natural: ((1/(1+0.75)*(0.5/(1+0.5+1.5))*4.0)/100)*5000 ≈ 19 mg
- cadmium yellow lemon: ((1/(1+0.75)*(1.5/(1+0.5+1.5))*4.0)/100)*5000 ≈ 57 mg
- titanium white: ((0.75/(1+0.75)*4.0)/100)*5000 ≈ 86 mg
- tempera: ((4.0*8.0)/100)*5000 = 1600 mg
- water: 5000-38-19-57-86-1600 = 3200 mg
|
Grl
Vert lion
|
Sina
Sienna nat
|
Tit
Titanium white
|
Egy
Egg yolk
|
H2O
Distilled water
|
|
|---|---|---|---|---|---|
| 0.76% | 0.38% | 1.14% | 1.71% | 32% | 64% |
So here we use three separate, nested rules of three to get a,b and two nested rules of three to get the white part. As far as recipe calculation goes, this is as complicated as it will get.
The important point is that by making the lum property dominant to the b:a c:a properties, a color transition towards white can be achieved by tweaking only the lum value and leaving the other properties unaffected. To summarize, let's make a general formula that allows us to make any amount of paint with any the properties that we have defined:
When making a total of pow | tem ∝ lum b b:a c c:a , we mix:
- a = ((1/(1+lum)*(1/(1+b:a+c:a))*pow)/100)*total
- b = ((1/(1+lum)*(b:a/(1+b:a+c:a))*pow)/100)*total
- c = ((1/(1+lum)*(c:a/(1+b:a+c:a))*pow)/100)*total
- white = ((lum/(1+lum)*pow)/100)*total
- binder = ((pow*tem)/100)*total
- solvent = total-a-b-c-white-binder
continuous progressions
Properties like lum and b:a are especially helpful when creating color transitions as you progress through the layers. For example, when transitioning from a darker to a brighter blue, four mixtures might be laid in consecutively where every recipe has a lum value that is higher than the last. Let's take a look:
|
Bpf
Bleu perm fonce
|
Tit
Titanium white
|
Egy
Egg yolk
|
H2O
Distilled water
|
|---|---|---|---|
| 0.05% | 3.6% | 34% | 62.35% |
|
Bpf
Bleu perm fonce
|
Tit
Titanium white
|
Egy
Egg yolk
|
H2O
Distilled water
|
|---|---|---|---|
| 0.11% | 3.73% | 33.4% | 62.79% |
|
Bpf
Bleu perm fonce
|
Tit
Titanium white
|
Egy
Egg yolk
|
H2O
Distilled water
|
|---|---|---|---|
| 0.36% | 3.5% | 32.6% | 63.54% |
|
Bpf
Bleu perm fonce
|
Tit
Titanium white
|
Egy
Egg yolk
|
H2O
Distilled water
|
|---|---|---|---|
| 1.3% | 2.73% | 32% | 63.97% |
The layers are always presented chronologically from bottom to top. The first thing to notice is that the power remains roughly the same. The temper will increase slightly, it climbs from 7.9 to around 9.3. The luminosity however climbs exponentially:
- first layer: 2.73/1.3 ≈ 2
- second layer: 3.49/0.36 ≈ 10
- third layer: 3.73/0.11 ≈ 34
- fourth layer: 3.59/0.05 ≈ 72
|
|
This has a number of advantages. Firstly, while working on a transition you can stop at any point and pick up right where you left off weeks or months later. Tempera paint goes bad in just a few days, and having a stored transition makes it easy to work at your own pace instead of needing to worry about this. What is especially interesting about this approach is that when using a function there is an infinite amount of transitions at your disposal, depending on how many points on your curve you wish to call in.
|
|
|
- move up-dow (mud): ƒ(x) = (x2)+mud
- move left-right (mlr): ƒ(x) = (x+mlr)2
- steepness (steep): ƒ(x) = (steep*x)2
- zoom (zoom): ƒ(x) = (x2)*zoom
- raise (raise): ƒ(x) = xraise
Which gives us in an overall formula:
- ƒ(x) = (((steep*(x+mlr))raise)*zoom)+mud
A linear function can be made by setting the raise parameter to 1. If you want to see for yourself how this works, try the graph plotter. All properties of interest can be bound to a function and then scaled to preference, the formulas always remain the same. In this way it is possible to define an entire painting as a set of continuous recipes before even starting.
to conclude
It was my aim to give you some appreciation for how the work is made and to make you able to understand the information that is given in the toggle tree under each painting. The math applied here is very basic and the theory was not developed as a concept behind the work but as a solution to practical problems I encountered across the years in my many failures.In practice there are many additional challenges that need to be handled. Mixing paint is an artform in and of itself. Keeping tiny amounts of dust and dirt out of your paints and paintings is also a constant challenge. When it comes to painting, there is plenty of literature out there that covers this topic in great detail. Daniel V Thompson's books 'The practice of tempera painting' and 'Materials and techniques of medieval painting' are two fantastic references to start out with. Another interesting book is 'Materials for a History of Oil Painting' by Charles Lock Eastlake.
alternative notations
Gessos and inks use other notations.
bindersystems
I will now proceed to cover some topics that are on the fringe of theory and practice. In theory it would be a more rigorous and elegant setup to work with multiple whites and binders by using more ratios and properties. In practice it has proven to be easier to work with fixed combinations of ingredients, because those values rarely need to fluctuate within a single painting. When working with multiple binders, the fat over lean rule must be respected for each binder separately. Every bindersystem has three fixed binder recipes, and one 3-component whiting system. Let us again turn to an example and compare two bindersystems and how they affect the compostition of the mixtures.
|
warp
To finalize and define the general formulas needed to calculate any amount of any mixture we will need to cover one last property. Warp is a property that creeps into all calculations and I have therefore decided to introduce it at the end to avoid complexity while explaining other concepts. In reality all pigments will have different densities and when measured on a weighing scale, result in very different volumes. The temper of a mixture will in practice work by volume and not by weight. By weight, a heavy pigment would have far too much binder in the mix compared to a lighter pigment, which would have too little. An accurate measuring system by volume is not very practical, but there is a quick fix for this problem. By introducing a weight-to-volume conversion table, every pigment will get a correction in the calculation to compensate for the density.
- Warp (warp) is the weight of a certain volume of pigment divided by the weight of that same volume of water
At this point we cross over from pure theory to handling a practical problem because every conversion table will only be as accurate as the calibration process was.
This cross-section shows all the different types of paint layers as they are layed in. The main idea is to use a predefined model of paint recipes to describe the passage from dark to light of a body in a single color, rather than to observe and suggest a play of light by mixing colors on a palet according to a color-wheel of some sort and using your intuition and experience to call it as you see it.
The model makes use of all the effects that tempera can offer.
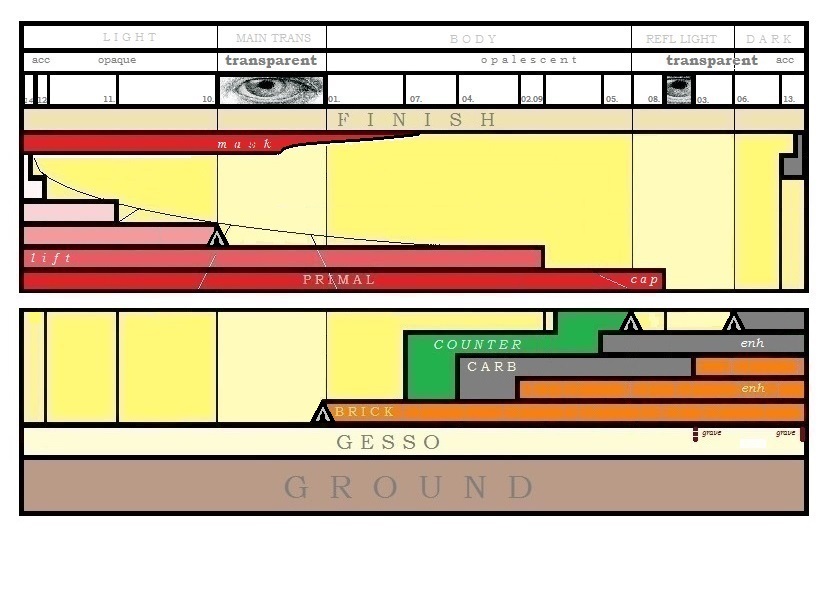
These effects are:
- Opaque
- Transparent
- Opalescent